
Puzzle
You must defeat a surprisingly intelligent rooster in a battle of wits involving 4 piles of corn kernels. There are only 3 rules of battle:
- You and the rooster each take turns picking up kernels of corn, with you going first.
- Each turn consists of taking a positive number of kernels from a single pile.
- The one who takes the last kernel wins.

Try the interactive version of the puzzle here!
Proof of Winning Strategy
Before we start with a proof of the winning strategy, let’s define
one term which will be used extensively throughout this page:
nim-sum. The nim-sum of a set of numbers is simply the result of
applying bitwise XOR ⊕ over the entire set. For example, the
nim-sum of 4, 5, and 6 is equivalent to 100 ⊕ 101 ⊕ 110 = 011 = 3.
For our proof of the winning strategy, we will need to prove three
intermediary lemmas:
-
The winning move always results in a position where the nim-sum is 0
-
If the nim-sum of a position is already 0, then there is no valid move that results in a position with a nim-sum of 0
-
If the nim-sum of a position is not 0, there always exists a move that results in a position with a nim-sum of 0
Lemma #1: The winning move always results in a position where the nim-sum is 0
This lemma is trivial. Simply notice that a winning move results in there being 0 kernels left in all piles. The nim-sum of any set made up entirely of 0s is 0.
Lemma #2: If the nim-sum of a position is already 0, then there is no valid move that results in a position with a nim-sum of 0
To prove this lemma, let’s first assume that there exists a valid move from a position with a nim-sum of 0 to a position with a nim-sum of 0. Let N-p be the nim-sum of all piles except for pile P, the pile in which this move occurs. Additionally, let k be the number of kernels in P, and k’ be the number of kernels in P after the above move is played.
If all of the above is true, then it holds that both k ⊕ N-p= 0 and k’ ⊕ N-p= 0. Combining the equations gives k ⊕ N-p ⊕ k’ ⊕ N-p = k ⊕ k’ = 0. This is true if and ONLY if k’ = k. Taking 0 kernels from a pile is not a valid move, so the lemma is proven.
Lemma #3: If the nim-sum of a position is not 0, there always exists a move that results in a position with a nim-sum of 0
This lemma is a little more involved. First, let’s define the shorthand Xy. This is the value of the bit in position y of X’s binary representation. We’ll additionally define N to be the nim-sum of all of the remaining piles, and i to be the position of the most significant 1 bit in N.
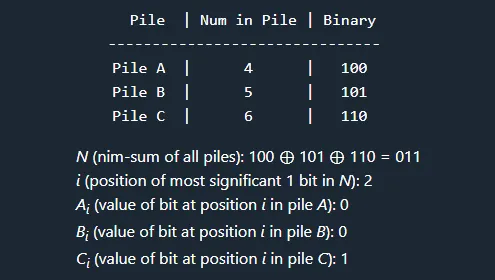
Using the above definitions, there must exist at least one pile P where Pi = 1. This is due to the fact that if all piles had a 0 in their ith position, then Ni would also be 0, contradicting our definition of i. We will play in this pile, and reduce the number of kernels in P from k to k’. We can construct a k’ that forces the resulting nim-sum of all the piles N’ to be 0 by simply setting k’ = k ⊕ N. (Intuitively, we just flip the value of bits in k at any position j where Nj = 1. This ensures that N’ = 0). Since Pi = 1 and Ni = 1, the most significant bit that is changed in the transformation from k to k’ will always be flipped from 1 to 0, ensuring that k’ < k. Thus, in a position where the nim-sum is not already 0, we can always play a move that results in a nim-sum of 0 by by reducing the number of kernels in pile P from k to k’.
Putting it all together
Combining all three lemmas reveals the winning strategy: on each
of your turns, play a move which results in a position with a
nim-sum of 0. This is is guaranteed to exist if the position does
not already have a nim-sum of 0 (lemma #3). Your opponent will be
forced to play a move that results in a non-zero nim-sum (lemma
#2). This cycle will continue until the winning move is played.
Since the winning move must result in a position with a nim-sum of
0 (lemma #2), you will always win!
If you found this breakdown interesting and would like to learn
more, check out the Wikipedia page on Nim!
Implementation
This puzzle’s implementation is quite straightforward - on each of the rooster’s turns, the nim-sum of the position is calculated. If the nim-sum is non-zero, a move derived from the strategy defined above is played. If the nim-sum is already 0, then a random move is played. During the initial setup, the amount of kernels in each pile is randomized. If the resulting position happens to have a nim-sum of 0, one kernel is added to a random pile, ensuring that the player always has a winning strategy if they play optimally.
