Puzzle: The Sneaky Rat

The Puzzle

There’s a rat on the loose in your 8 house neighborhood, and it’s your job to catch it! The rat starts in a random house and moves to an adjacent house every night. Houses 1 and 8 are not considered adjacent. Each day you are allowed to trap two houses - if the rat is in one of the two houses you trap, it will be caught. If you trap houses 1 and 2 on the first day, 2 and 3 on the second day, and so on, you are guaranteed to catch the rat in at most 7 days. This, however, is not optimal - what trapping strategy is guaranteed to catch the rat in the fewest number of days?

Try the interactive version of the puzzle here!

Solution

To start, let’s assume that the rat begins in an even numbered house, i.e. houses 2, 4, 6, or 8. On the first day, we trap houses 2 and 4. If we don’t catch the rat, that means the rat started in house 6 or 8. Now, notice that the only houses adjacent to house 6 and 8 are houses 5 and 7. Since the rat has to move to an adjacent house each day, we can trap houses 5 and 7 on the second day, guaranteeing that we will catch the rat if it started in an even numbered house. If we don’t find the rat on day 2, we can definitively conclude that the rat started in an odd numbered house!

If the rat started in an odd numbered house, then on the third day it will also be in an odd numbered house (notice that the parity of the house number the rat is in flips each day). Thus, we can employ a similar strategy to before: on day 3, we check houses 5 and 7. If we don’t find the rat, then the rat must have been in houses 1 or 3. Since the only houses adjacent to houses 1 and 3 are houses 2 and 4, we check those houses on the fourth day, guaranteeing that we catch the rat in only four days!

Implementation

The crux here is how to programmatically verify if a submitted arrangement of traps will successfully catch the rat. In this case where there are only 8 houses and a maximum of 7 days, it would be completely feasible to enumerate all 316 possible paths the rat can take, then check if all those paths run into a trap using the submitted arrangement. That’s inefficient and lame though! Let’s think of something a little more elegant.

We can think of a submitted solution as a graph with “layers”, where each layer corresponds to a day. Within a day / layer, we represent each house as a node. The edges will represent how the rat can move between days - for example, house 2 in the first layer will have two outgoing edges - houses 1 and 3 in the second layer. Connect all nodes in the first layer to a start node, and all nodes in the last layer to an end node.

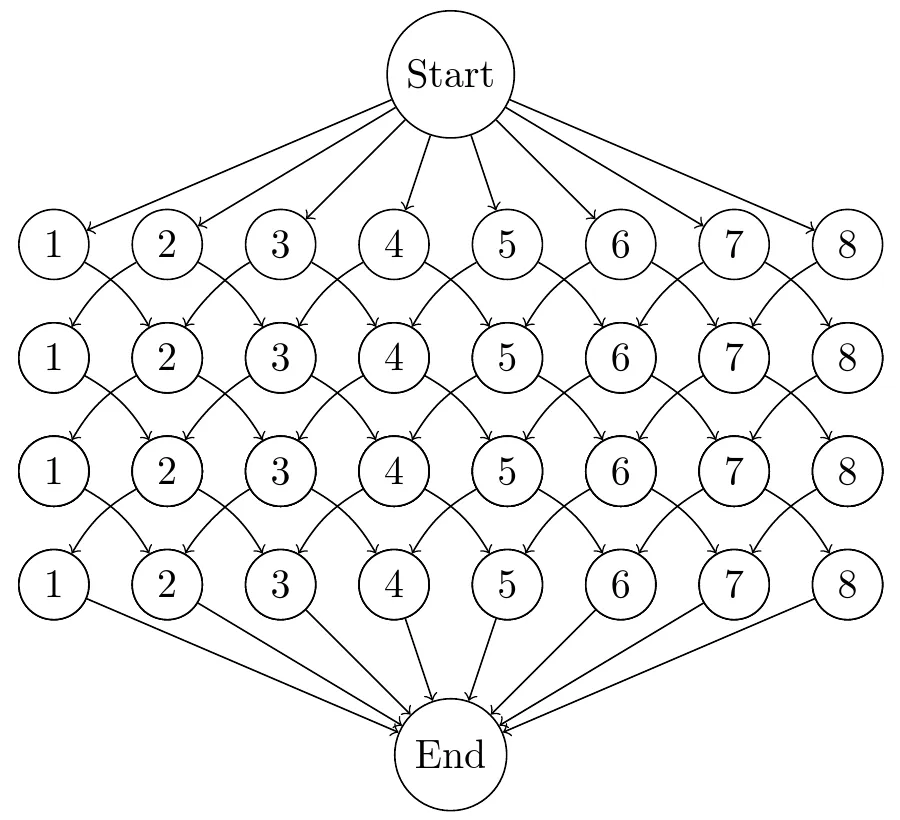
To check if a submitted solution is guaranteed to catch the rat, simply remove the nodes corresponding to trapped houses from the graph. Check if there still exists a route from the start node to the end node using a simple path finding algorithm. If such a path no longer exists, the submitted solution is guaranteed to catch the rat!

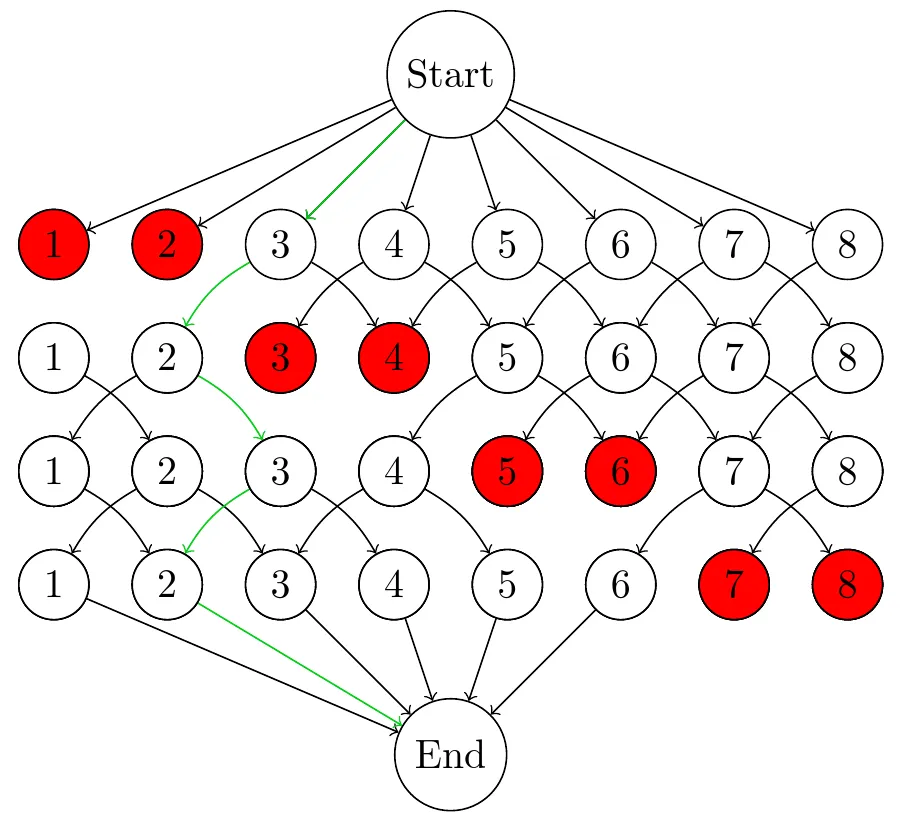
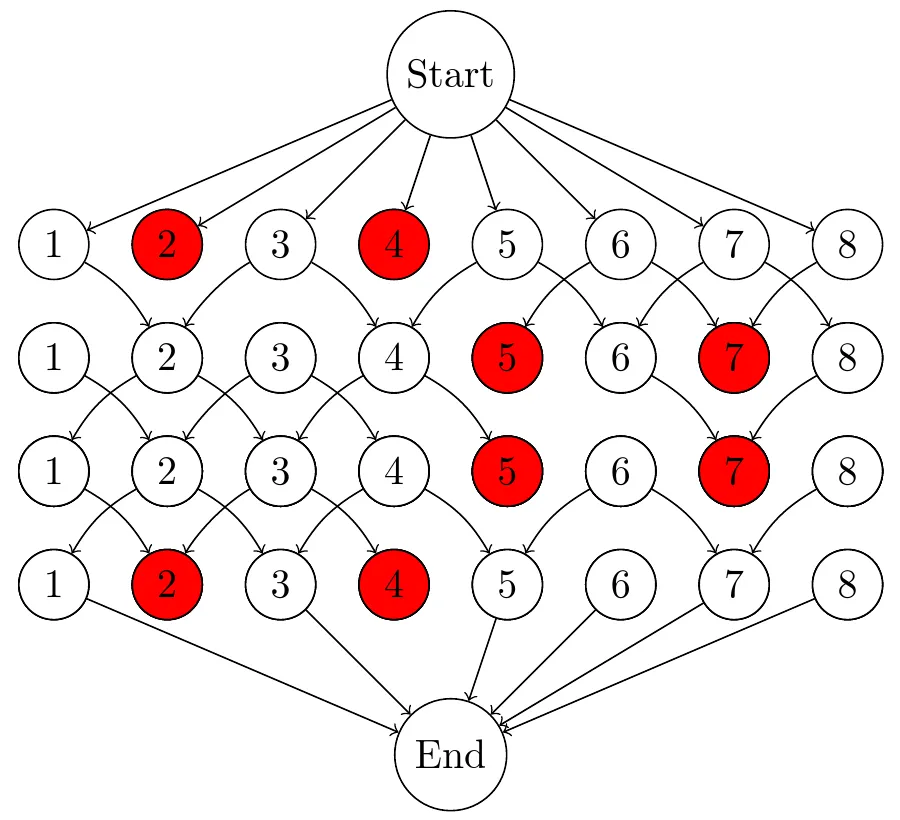
Bonus Puzzle

Can you determine how many days it would take to catch the rat in a neighborhood with an arbitrary number of houses?

Solution

To calculate how many days it would take to catch the rat for an arbitrary number of houses, we again make use of odd / even idea introduced in part 1. This time we begin from the last day, work backwards to eliminate half of the houses in a row (i.e. all odd or even houses), then continue on in the same manner until all houses in a row are eliminated. In the 11 house example below, red nodes represent rat-trapped houses, and yellow nodes represent houses in which the rat is guaranteed to run into a rattrap in the future.

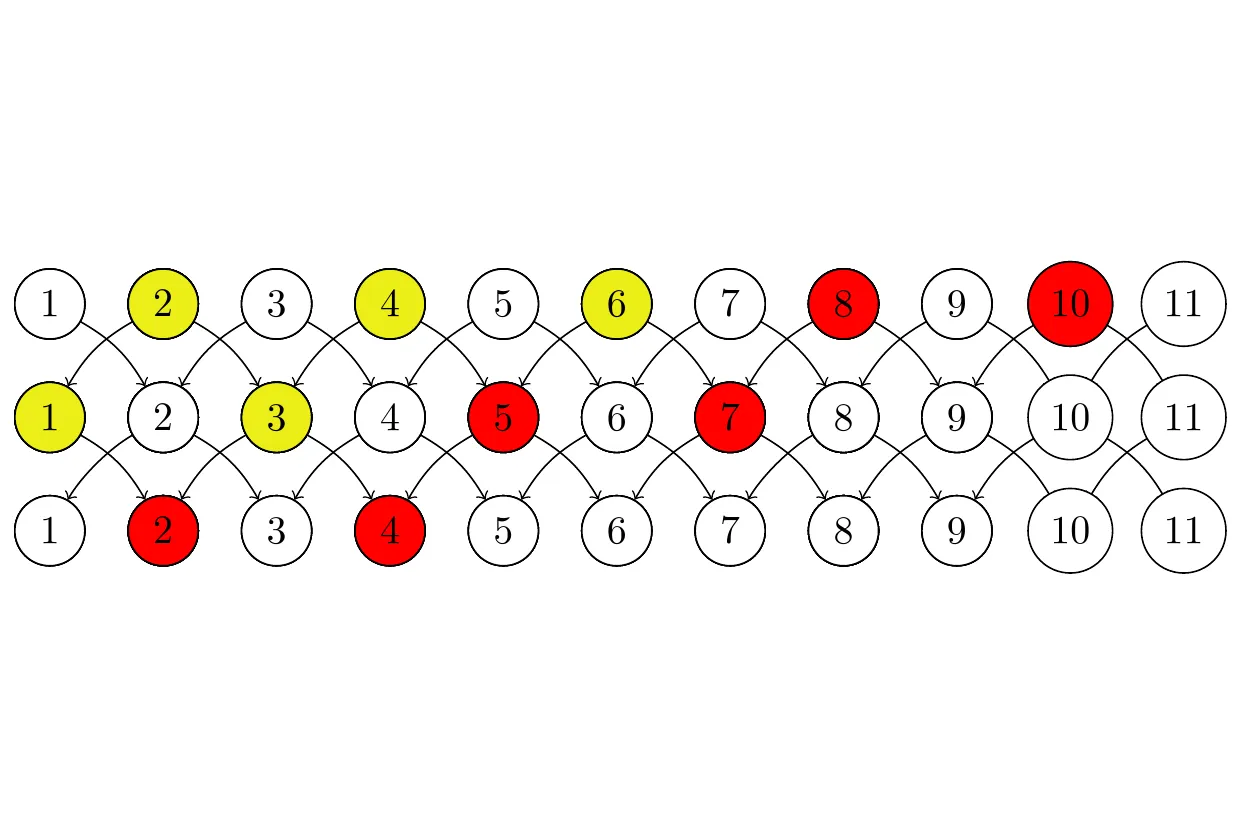
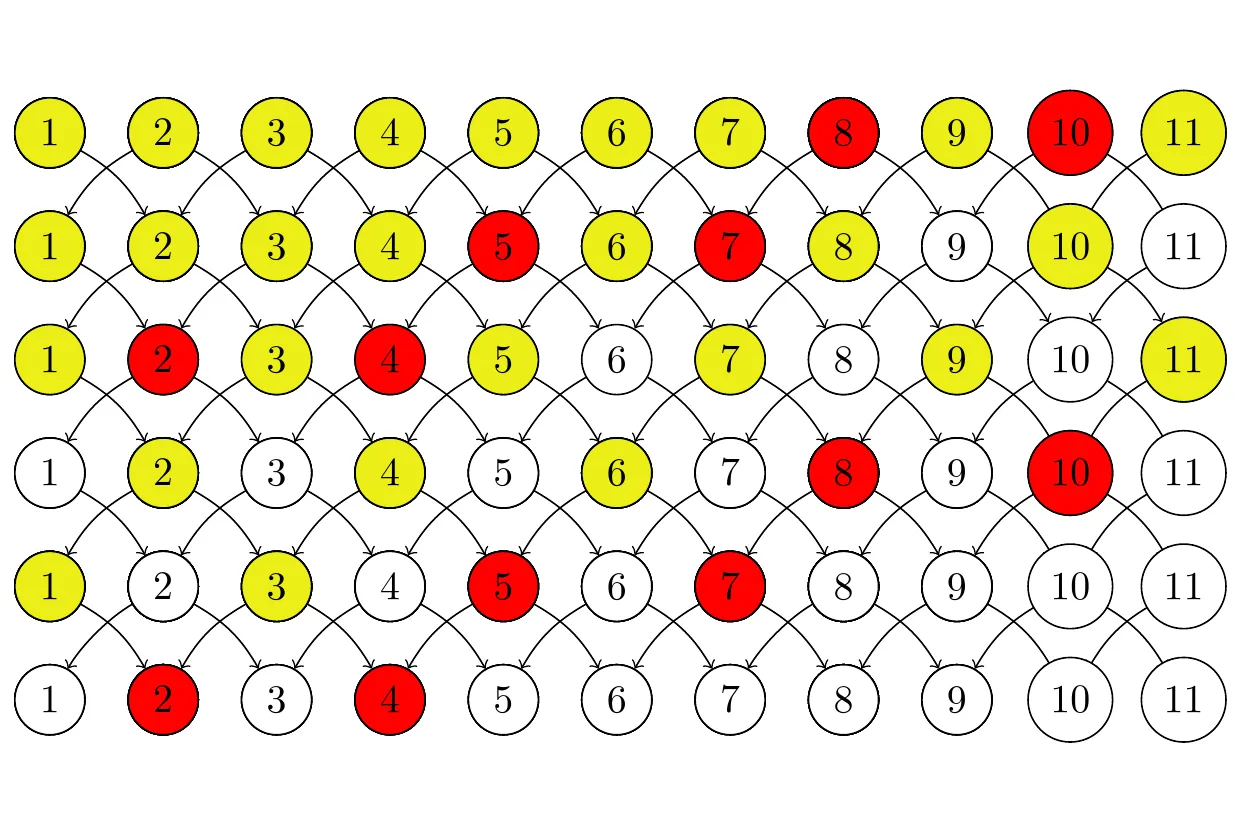
The number of days needed to eliminate half the houses is X_1/2 = Floor(# of houses / 3). The number of days needed to eliminate the rest of the houses is, in most cases, also X_1/2. The one exception is when X _1/2 is even, and the number of houses is divisible by 3. In this case, the number of days needed to eliminate the rest of the houses is X _1/2 - 1. This is because if the number of houses is divisible by 3, then on on day X_1/2 half the houses are eliminated after one trap is placed, so the other trap is used to get a head start on eliminating the rest of the houses. This head start will only make a difference if X _1/2 is even.

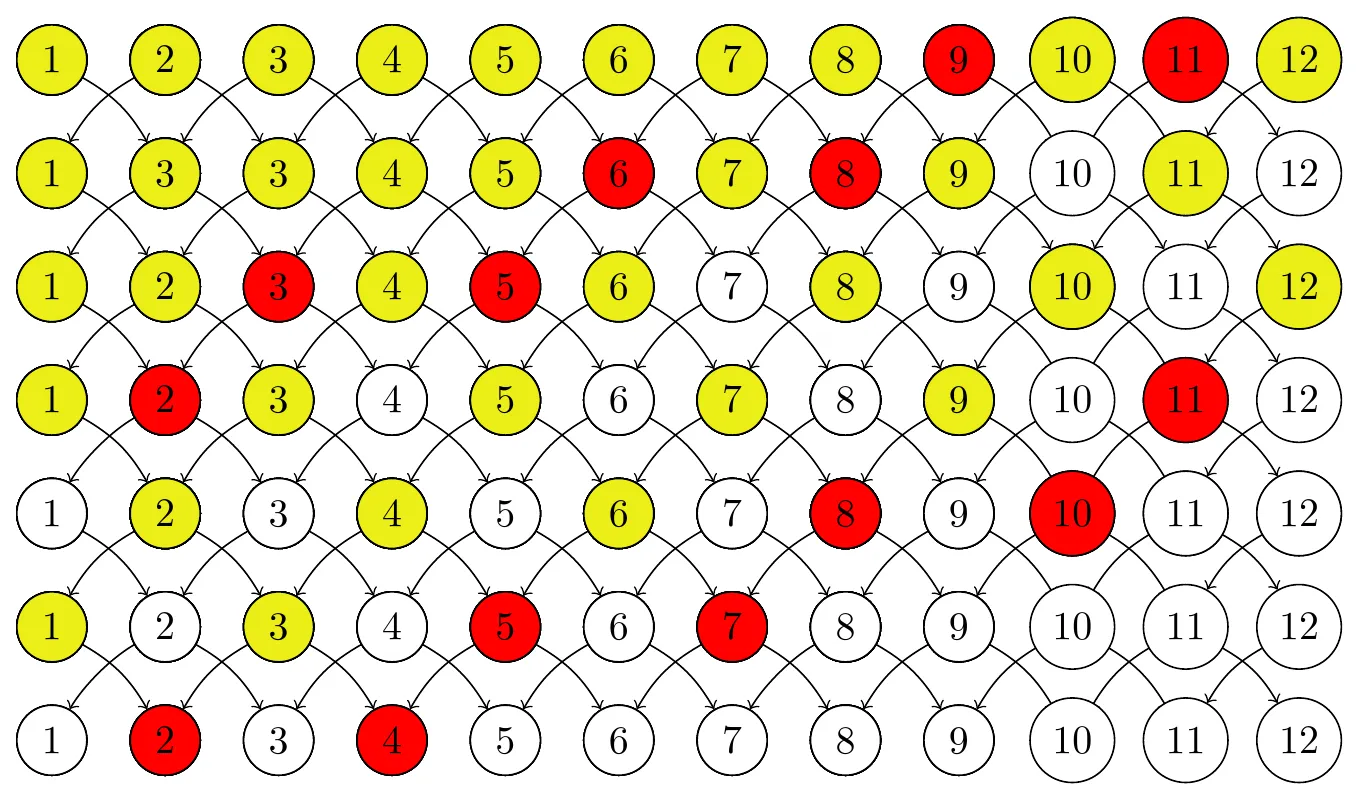
Thus, the number of days needed to catch the rat for any number of houses N is given by the expression 2X_1/2 - 1 if X_1/2 is even and N is divisible by 3, and the expression 2X_1/2 otherwise. This is the precise formula used to validate if a submitted answer to part 2 is correct in the interactive puzzle.