
The Puzzle
You need to figure out the fastest 3 horses from a group of 25. You can only race 5 horses at a time to find their relative speeds - timing the horses or finding their absolute speeds by other methods is not allowed. What is the minimum number of races it takes to find the fastest 3 horses?
Try the interactive version of the puzzle here!
Solution
The solution to this puzzle is reminiscent of a multi-way merge sort. To start, 5 ordered lists of horses are attained by conducting 5 races in which every horse is raced exactly once. A 6th race is conducted with the winners of the previous 5 races. The winner of this race is guaranteed to be the fastest horse. A 7th race is conducted, replacing the winner of the 6th race with the horse that came directly behind it in its original group. The winner of this race is guaranteed to be the second fastest horse. An 8th race is constructed in the same fashion - the winner of the 7th race is replaced with the horse that came directly behind it in its original group The winner of this race is guaranteed to be the third fastest horse. Thus, we have found the fastest 3 horses in only 8 races!
But wait, we can optimize this solution and do slightly better! First, let’s define group 1 as the 5 horses the winner of race 6 was initially grouped with, group 2 as the 5 horses the runner-up of race 6 was initially grouped with, and so on. Notice that ALL horses from groups 4 and 5 already have at least 3 horses that are faster than them. Therefore, we should exclude them from any future races, as these horses cannot be the 2nd or 3rd fastest. In fact, after the 6th race, there are only a couple horses that have the potential to be the 2nd or 3rd fastest:
-
If all three fastest horses were placed into the same initial group:
- The 2nd and 3rd fastest horses must be the 2nd and 3rd place finishers of group 1.
-
If the two fastest horses were placed into the same initial group:
- The 2nd and 3rd fastest horses must be the 2nd place finisher of group 1 and the 1st place finisher of group 2.
-
If the second and third fastest horses were placed into the same initial group:
- The 2nd and 3rd fastest horses must be the 1st and 2nd place finishers of group 2.
-
If the fastest and third fastest horses were placed into the same initial group:
- The 2nd and 3rd fastest horses must be the first place finisher of group 2 and the 2nd place finisher of group 1.
-
If none of the fastest three horses were placed into the same initial group:
- The 2nd and 3rd fastest horses must be the winners of groups 2 and 3.
Notice that there are only 5 distinct horses vying for the remaining two spots in the trifecta - the 2nd and 3rd place finishers from group 1, the 1st and 2nd place finishers from group 2, and the 1st place finisher from group 3. Thus, for our 7th race, we can simply race these 5 horses and declare the fastest two the second and third fastest horses! We’ve now found the fastest 3 horses in just 7 races, the optimal solution!
Implementation
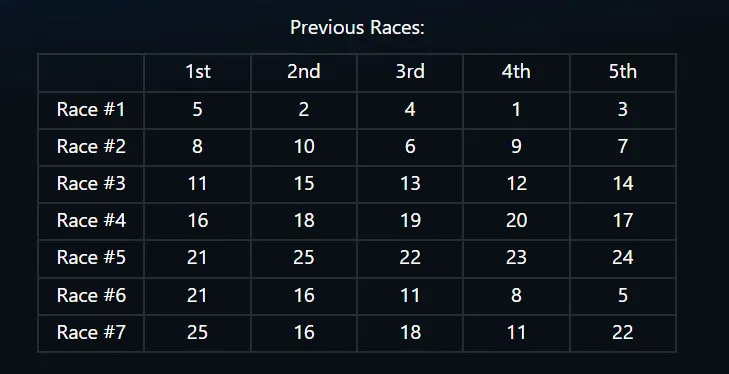
The crux of implementing this puzzle is to, given a series of races, determine if the submitted horses must be the fastest 3. We can verify this by constructing a simple graph. We start by creating 25 nodes, one for each horse. For each horse in each race, we draw an edge to the horse it finished directly in front of. Now, if there is exactly one source (a node with no incoming edges) in the resulting graph, then the horse corresponding to that node must be the fastest horse included in the graph.
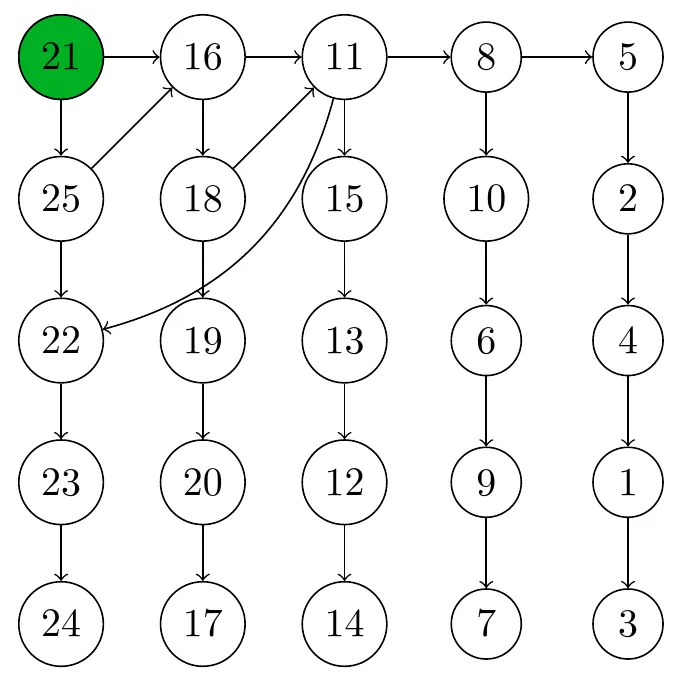
To check that the submitted 2nd fastest horse must indeed be the 2nd fastest horse, simply remove the fastest horse from the graph and again check if there is only one source. This process can be repeated any number of times.
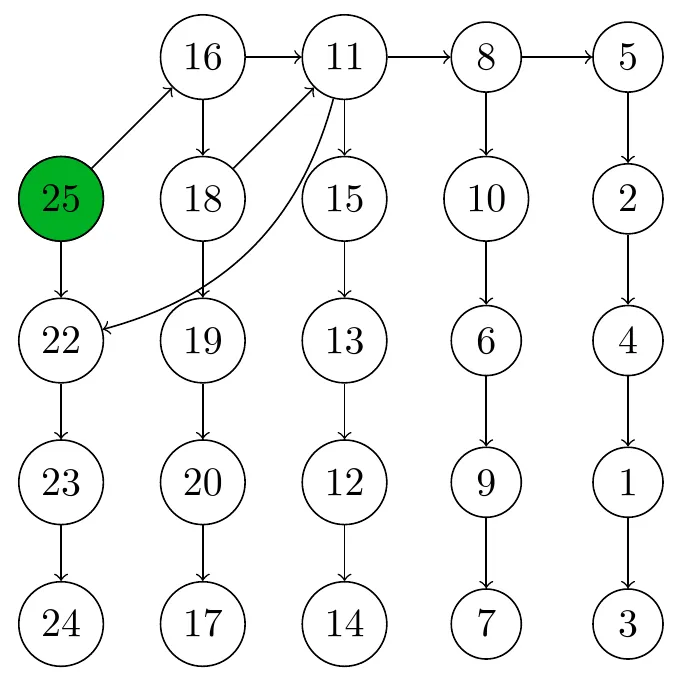
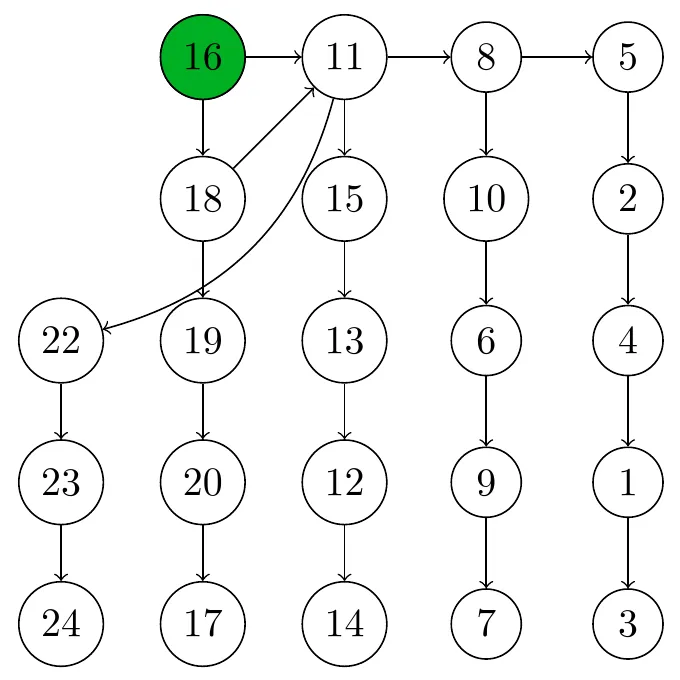
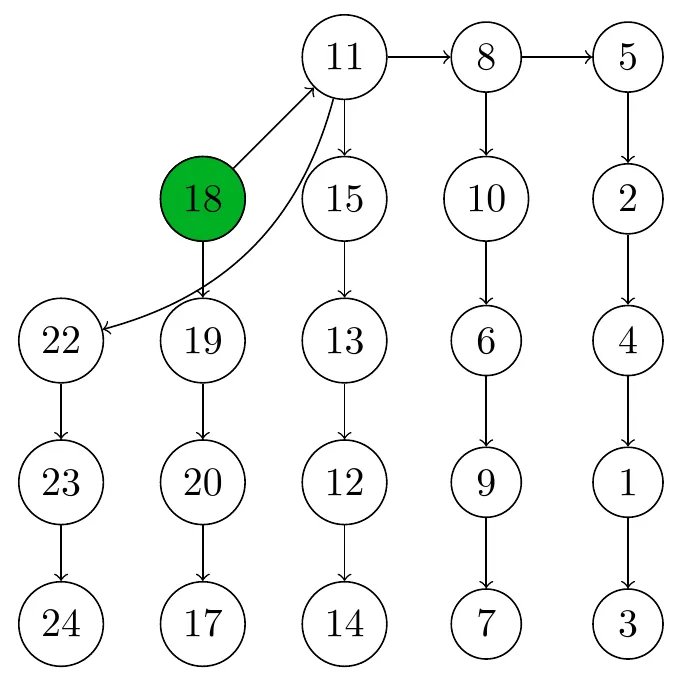
Note that, in this specific example, we actually get to know the fastest 4 horses after just 7 races! This is not always the case - this specific configuration was just lucky. If there are multiple source horses, it means that the speed relation between said horses is ambiguous. An example is shown below:
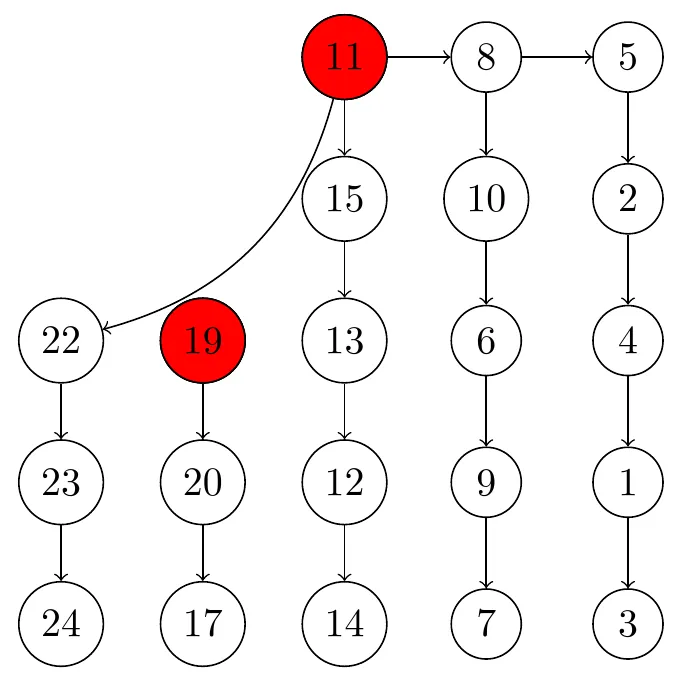
If such a situation happens while determining the 1st, 2nd, or 3rd fastest horse, then the submitted trifecta / series of races is invalid!
